基于Transformer的自然语言生成模型
一些 Transformer 学习笔记。
以下说法多为特例,勿视为通用情况。
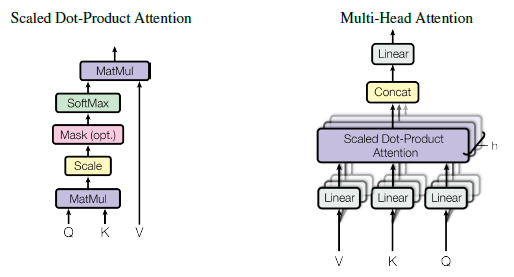
多头注意力机制
- 查询序列:${\pmb Q}=[{\pmb q}_1;{\pmb q}_2;…;{\pmb q}_N]^\top \in {\Bbb R}_{N\times d}$,用于检索上下文信息。
- 键值序列:查询序列关注的对象,实际包含两个序列,构成键值对$({\pmb K},{\pmb V})$。
- 键矩阵${\pmb K}=[{\pmb k}_1;{\pmb k}_2;…;{\pmb k}_M]^\top \in {\Bbb R}_{M\times d}$
- 值矩阵${\pmb V}=[{\pmb v}_1;{\pmb v}_2;…;{\pmb v}_M]^\top \in {\Bbb R}_{M\times d}$
点乘注意力(Dot-Product Attention):$\beta_{i,j}={\pmb q}_i\cdot{\pmb k}_j$
注意力分数归一化:$\alpha_{i,j}={\rm softmax}({\pmb q}_i,{\pmb k}_j)$
第$i$个位置的上下文向量:${\rm Dot\_Attention}({\pmb q}_i,{\pmb K},{\pmb V})=\sum_{j=1}^M \alpha_{i,j} {\pmb v}_j$
综上:$${\rm Attention}({\pmb Q},{\pmb K},{\pmb V})={\rm softmax}({\pmb Q}{\pmb K}^\top){\pmb V} \in {\Bbb R}_{N\times d}$$
缩放点乘注意力(Scaled Dot-Product Attention):随着隐向量维度$d$增大,${\pmb q}_i\cdot {\pmb k}_j$的方差也逐渐增大:
设${\pmb x}, {\pmb y}$为$n$维独立向量且${\rm var}({\pmb x})={\rm var}({\pmb y})=1$,${\rm E}({\pmb x})={\rm E}({\pmb y})=0$,则${\pmb x}\cdot{\pmb y}=\sum_{i=1}^n x_i y_i$的均值为0,方差为$n$。
为了解决归一化后注意力分布尖锐导致梯度消失的问题,提出缩放点乘注意力:$${\rm Attention}({\pmb Q},{\pmb K},{\pmb V})={\rm softmax}( \frac{ {\pmb Q}{\pmb K}^\top}{\sqrt{d}} ){\pmb V}$$
多头注意力(Multi-Head Attention):促使注意力能关注序列不同位置。将${\pmb Q},{\pmb K},{\pmb V}$通过$h$组映射矩阵${\pmb W}_i^q,{\pmb W}_i^k,{\pmb W}_i^v \in {\Bbb R}^{d\times d/h}$映射到$h$个子空间,进行注意力运算,再拼接,并通过输出映射矩阵${\pmb W}^O\in {\Bbb {R}}^{d\times d}$映射回原始空间${\Bbb{R}}^{N\times d}$:
$$
\begin{array}
\\
{\pmb H}_i={\rm Attention}({\pmb Q}{\pmb W}_i^q,{\pmb K}{\pmb W}_i^k,{\pmb V}{\pmb W}_i^v)\\
{\rm MHA}({\pmb Q},{\pmb K},{\pmb V})=({\pmb H}_1\oplus{\pmb H}_2\oplus…\oplus{\pmb H}_h){\pmb W}^O
\end{array}
$$
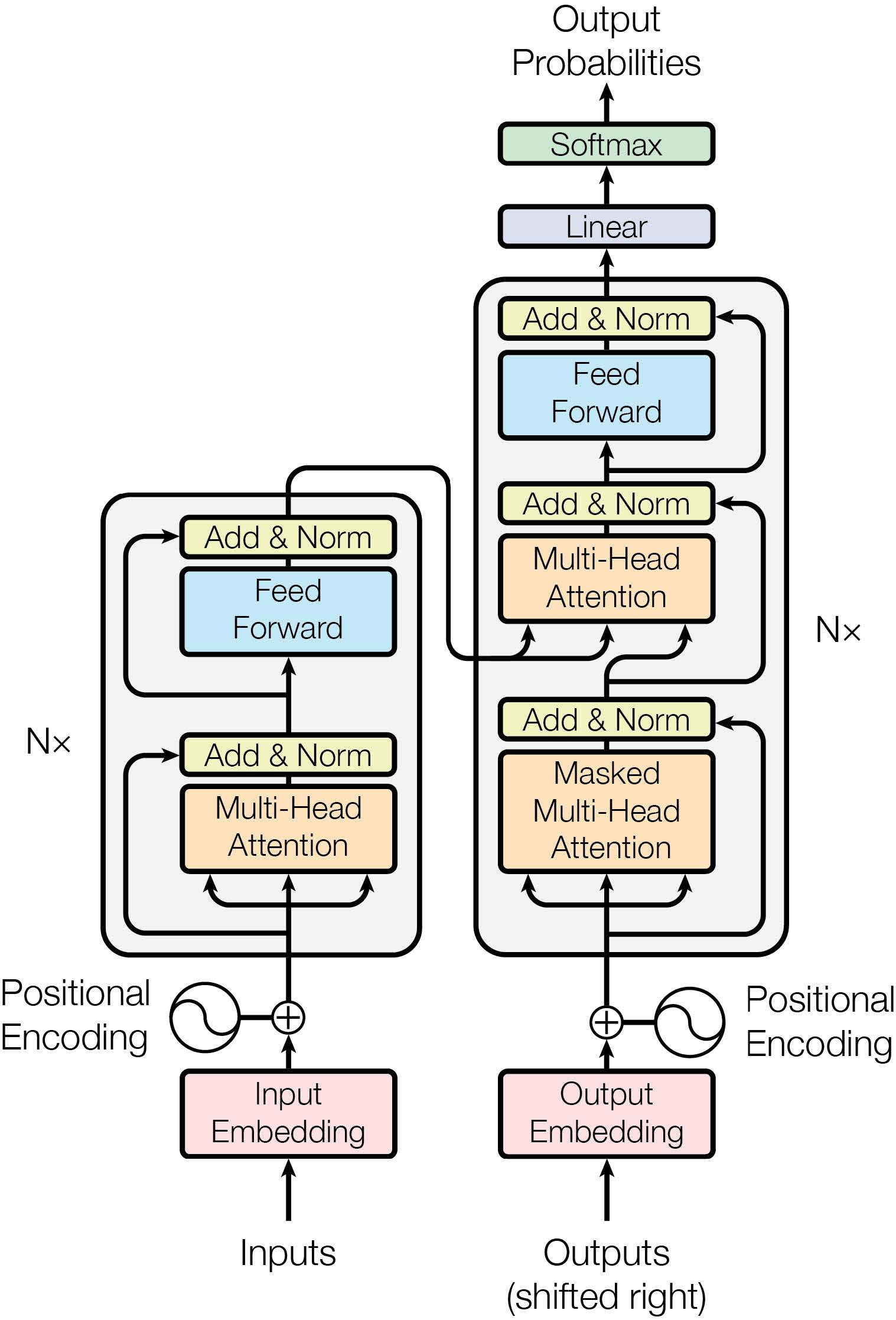
Transformer基本单元
Transformer基本单元主要由两部分构成:
- 第一部分由多头自注意力机制、残差连接与层归一化组成。
- 第二部分由前馈全连接网络、残差连接与层归一化组成。
形式化表示为:
$$\begin{array}
\\
{\pmb H}_{(1)}^l = {\rm{LayerNorm}}({\rm{MHA}}({\pmb H}^l,{\pmb H}^l,{\pmb H}^l)+{\pmb H}^l)\\
{\pmb H}^{l+1} = {\rm{LayerNorm}}({\rm{FeedForward}}({\pmb H}_{(1)}^l)+{\pmb H}_{(1)}^l)
\end{array}$$
下面具体介绍各个模块。
- 多头自注意力(Multi-Head Self Attention)机制:输入序列${\pmb{H}}$同时作为${\pmb{K}}$, ${\pmb{Q}}$, ${\pmb{V}}$,通过计算序列对其自身各个位置的注意力分布来建模序列的依赖关系,从而获得输入序列的上下文表示。
- 残差连接(Residual Connection):一般附加在另一模块之上,将该模块的输入${\pmb x}$与输出$f({\pmb {x}})$相加。此方法能够在模型层数较多时,将模型底层信息转递到模型的高层,一定程度上缓解梯度消失的问题。
- 层归一化(Layer Normalization):对输入的向量进行归一化操作。设输入向量${\pmb x}=[x_1,x_2,…,x_d]$的维度为$d$,利用其均值$\mu$和方差$\sigma$作归一化,使得特征的方差在不同深度的模块中保持一定的范围,让梯度更加稳定:$${\rm {LayerNorm}}({\pmb x})=\frac{\pmb g}{\sigma}\otimes({\pmb x}-\mu)+{\pmb b}$$其中${\pmb g}$和${\pmb b}$为可学习的权重向量。
- 前馈网络(Feed-Forward Network):$${\rm{FeedForward}}({\pmb x})={\rm ReLU}(x{\pmb W}_1+b_1){\pmb W}_2+b_2$$
Transformer结构
参考资料
[1] 黄民烈等. 《现代自然语言生成》. 电子工业出版社, 2021.
[2] The Annotated Transformer
本站所有文章除特別聲明外,均採用 CC BY-SA 4.0 協議 ,轉載請註明出處!