多模態知識可解釋性 Multimodal Knowledge Interpretability

本篇介紹三篇多模態知識可解釋性相關新近工作，這些工作做了多模態模型學習到的知識的可視化或分析性實驗。

Finding Structural Knowledge in Multimodal-BERT

ACL2022, arXiv:2203.09306

探究多模態模型嵌入（每層編碼器的輸入。最底層即輸入的embedding，其他爲前一層輸出的隱狀態）表示蘊含的結構知識。

研究問題

  • RQ 1: 多模態BERT的文本嵌入相比於文本BERT是否保留結構知識？
    • Sub-RQ 1.1：文本-圖像聯合訓練是否有影響？
  • RQ 2: 多模態BERT的視覺嵌入是否學習到如何編碼視覺場景樹（scene tree）？

主要貢獻

  • 根據文本依存樹，爲圖像定義場景樹
  • 利用結構探針（structural probe），輸入文本/圖像結點的模型嵌入，預測文本依存樹或圖像場景樹結點深度和距離

構建場景樹

Scene tree

輸入

  • 文本依存樹$T_t=\{ E_t, V_t \}$
  • 視覺短語（phrase，含圖像區域和對應文本）集合$P$
  • 圖像$I$

輸出

  • 場景樹$T_s=\{ E_s, V_s \}$ (根結點$v_{s,0}$爲$I$)
  • 結點之間的距離矩陣$\boldsymbol{D} \in \mathbb{D}^{n\times n}$
  • 結點深度向量$\boldsymbol{d} \in \mathbb{D}^{n}$。

結構探針

輸入：文本/圖像結點的嵌入
輸出：預測的文本依存樹/圖像場景樹距離矩陣、深度向量

  • 距離探針 $\boldsymbol{D}_{ij}=(\boldsymbol{B}(\boldsymbol{h}_i^l-\boldsymbol{h}_j^l))^\top(\boldsymbol{B}(\boldsymbol{h}_i^l-\boldsymbol{h}_j^l))$
  • 深度探針 $\boldsymbol{d}_{i}=||\boldsymbol{h}_i||_{\boldsymbol{B}}^2=(\boldsymbol{B}\boldsymbol{h}_i^l)^\top(\boldsymbol{B}\boldsymbol{h}_i^l)$

實驗

純文本：Penn Treebank (PTB3)
圖文：Flickr30k

模型

  • 文本：BERT
  • 單流：UNITER
  • 雙流：ViLBERT

基線：未作微調的zero-shot文本/圖像嵌入；原始RCNN特徵。

結論

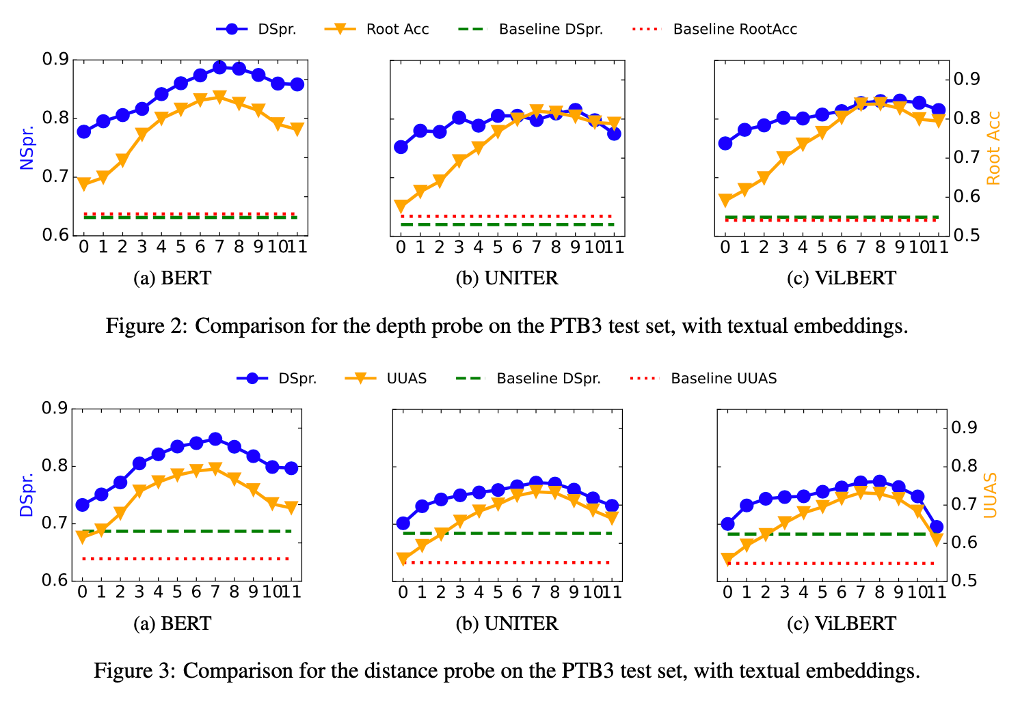
Text probe on PTB3

模型中間層嵌入蘊含更多結構知識。

RQ1結論：在PTB3數據集上，多模態模型保留的文本結構知識不及BERT。

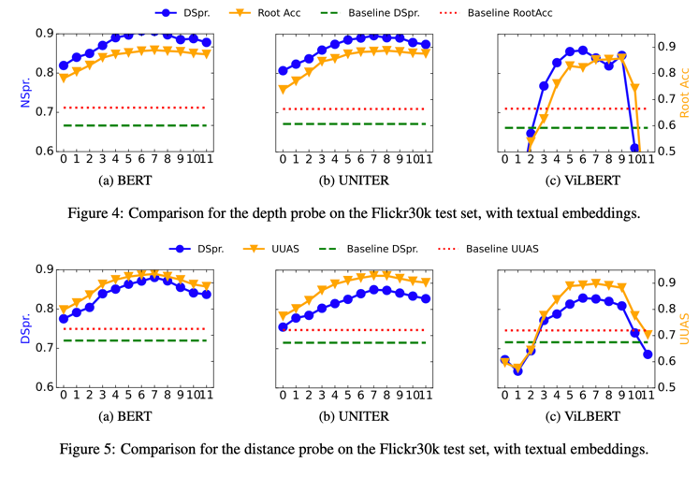
Text probe on Flickr30k

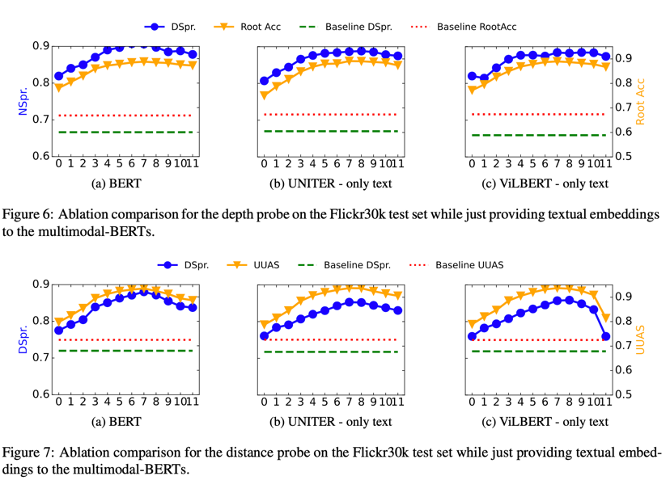
Text probe on Flickr30k w/o visual embeddings

Sub-RQ1結論：在Flickr30k數據集上，效果和BERT差不多，但並非視覺嵌入參與訓練的貢獻。

（合理懷疑：Flickr30k畢竟是圖文數據；PTB3可能跨領域了）

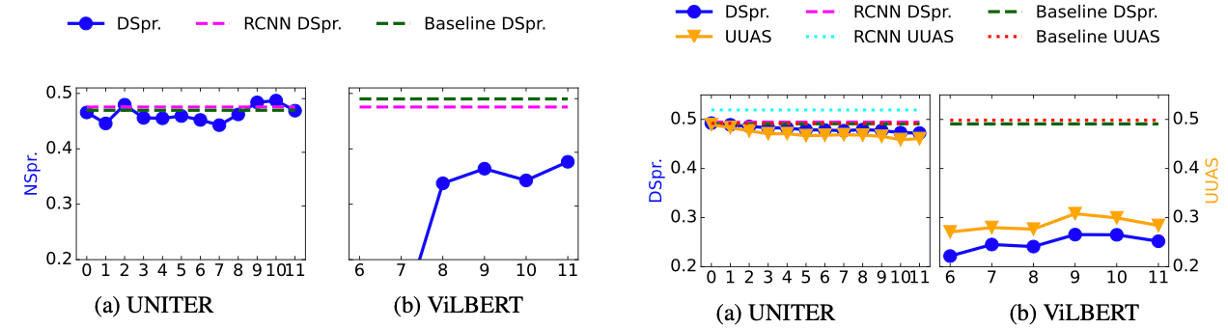
Visual probe on Flickr30k

RQ2結論：視覺嵌入構建場景樹的效果不如利用原始RCNN特徵。

VL-InterpreT: An Interactive Visualization Tool for Interpreting Vision-Language Transformers

arXiv:2203.17247

（單流）多模態Transformer注意力和表示的可視化工具

  • 注意力：考慮每層的注意力頭，以及跨模態/模態內注意力，構成大小爲$(N_{layers},N_{heads},L_{v}+L_{l},L_{v}+L_{l})$的注意力矩陣。對各層各注意力頭注意力權重、各token注意力權重可繪製熱力圖。
  • 隱狀態表示：t-SNE降維到2維，可視化。

對KD-VLP模型在兩個視覺問答任務VCR（Visual Commonsense Reasoning，視覺常識推理）和WebQA上做可視化分析（略）。

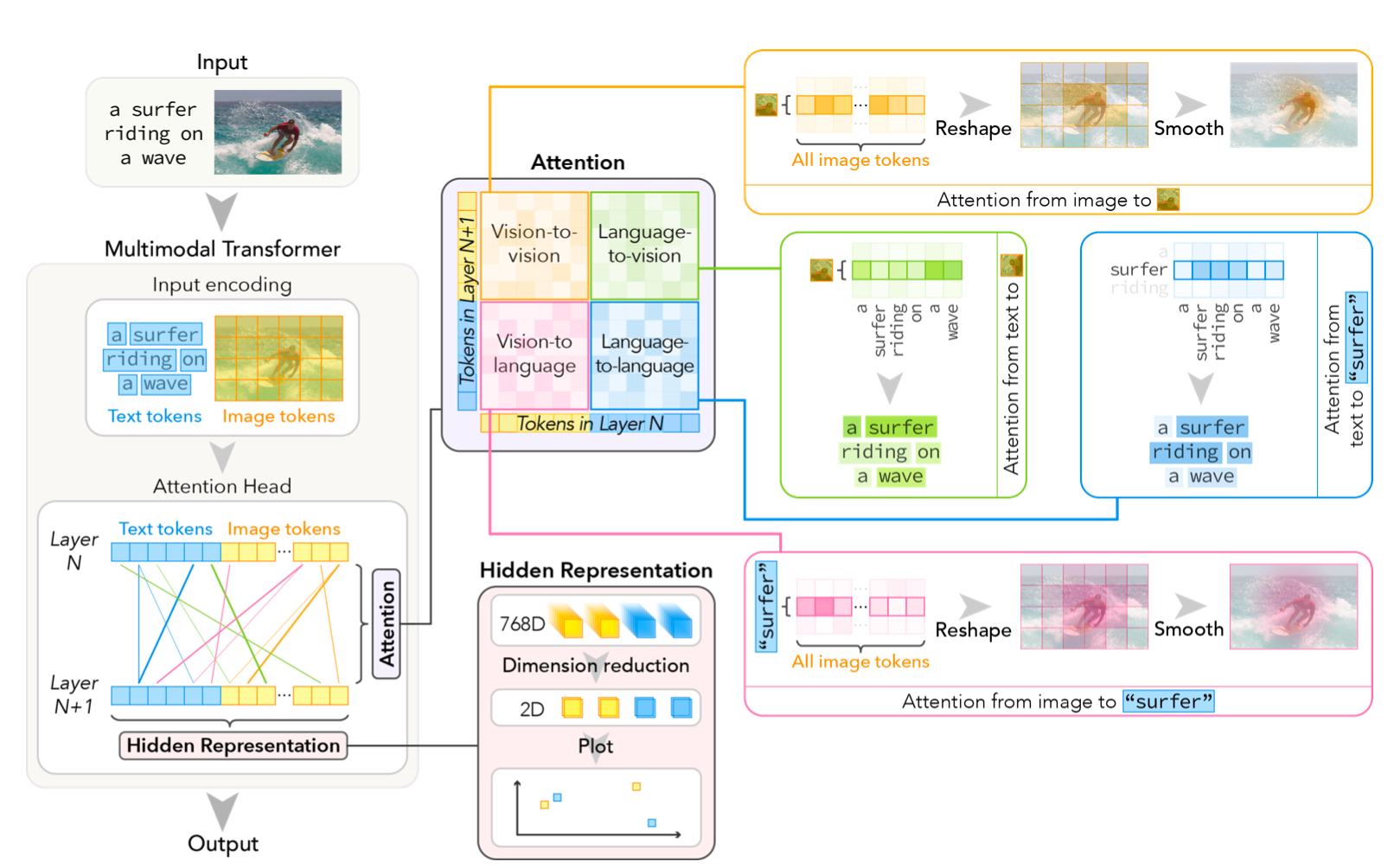
VL-InterpreT

Mind the Gap: Understanding the Modality Gap in Multi-modal Contrastive Representation Learning

arXiv:2203.02053

探究多模態表示空間的間隔。如CLIP一類雙流模型的模態表示間隔是由於不同的模型初始化和對比學習優化所造成；非線性激活函數可造成圓錐效應；改變模態間隔，可改善下游zero-shot分類性能並減少種族偏見。

對模態間隔現象提供三个方面的解釋：

  • 深度神經結構的歸納偏置（inductive bias）產生圓錐效應（cone effect）：無論是否預訓練過，模型的向量空間均被限制在狹窄的圓錐中。
  • 不同的隨機初始化產生不同的嵌入向量錐。
  • 對比學習目標函數保留了這個間隔。

理論分析表明，每個神經網絡層有大概率縮小了嵌入向量之間的角度，在更深的網絡結構下創建更窄的圓錐。

模態間隔

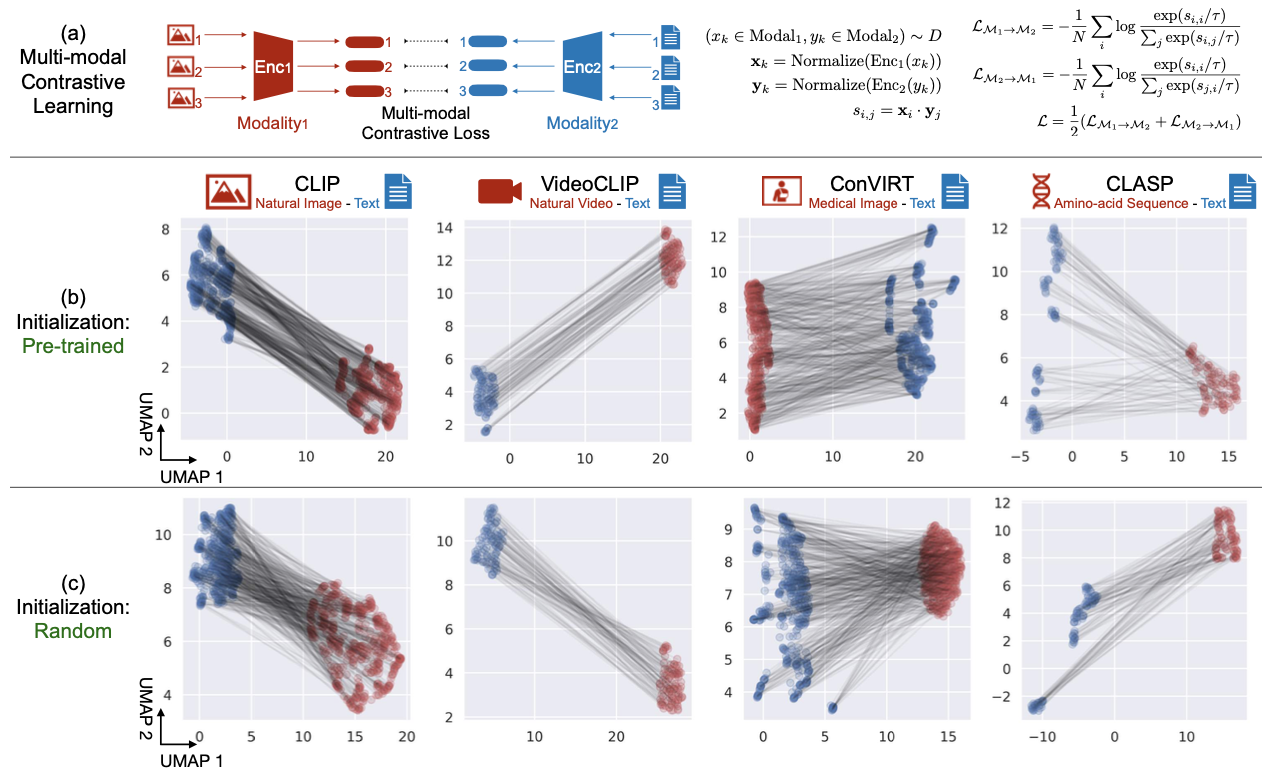
Modality gap

  • 各種模態的（雙流）模型
  • 隨機權重仍有此現象

圓錐效應致模態間隔

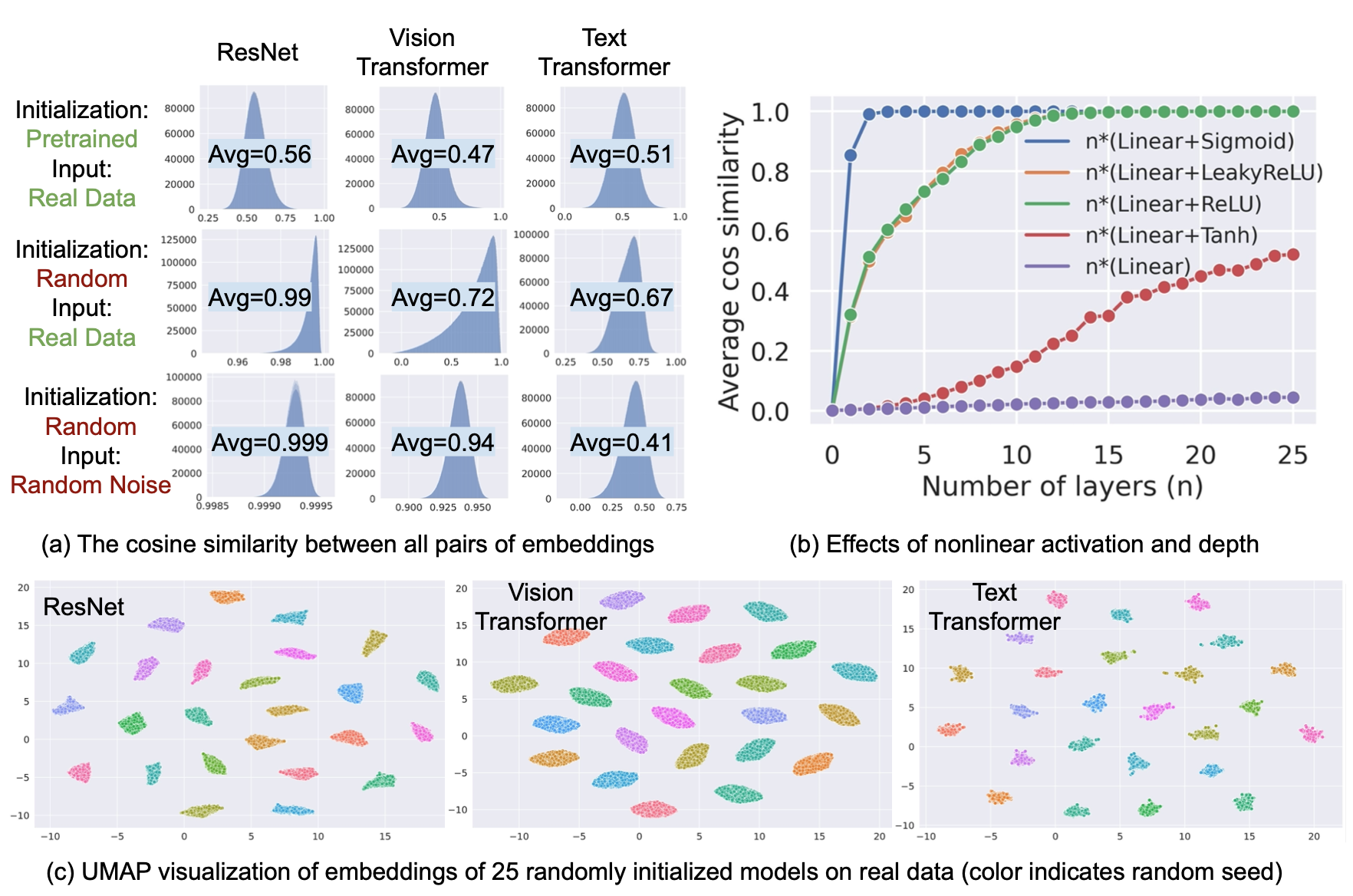
Cone effect

嵌入的狹窄圓錐

如上圖(a)：

  • 平均/最小相似度均爲正數
  • 隨機權重的模型也存在該效應，甚於預訓練過的
  • 隨機噪聲（視覺：正態分佈/文本：隨機數）+隨機權重的模型也存在該效應

結論：圓錐效應反映深度模型普遍的歸納偏置；先前工作的解釋稱「不平衡的詞頻分佈使優化有偏置」，不夠準確。

非線性激活函數的影響

如上圖(b)，考察各種MLP，無激活函數MLP隨層數增加圓錐效應不明顯，反之有激活函數的多層MLP餘弦相似度迅速上升（ReLU輸出非負，故餘弦相似度上升最快）。

結論：非線性激活函數對圓錐效應有重要影響。

層歸一化的影響待探究。

不同隨機初始化

如上圖(c)。

結論：不同隨機初始化產生不同的圓錐。

理論分析

對上述現象的數學證明（略）

  • 餘弦相似度隨層數加深逐漸增加
  • 中間層輸出的方差主要源於模型的不同隨機初始化

CLIP一類對比學習保留模態間隔

分析CLIP的InfoNCE中溫度$\tau$的影響。

定義模態間隔爲兩個模態嵌入表示中心點的歐氏距離

$$\vec{\Delta}_{\mathrm{gap}}=\frac{1}{n}\sum_{i=1}^n\mathbf{x}_i - \frac{1}{n}\sum_{i=1}^n\mathbf{y}_i$$

於是可調整根據間隔方向調整模態差距

$$
\begin{array} \\
\mathbf{x}_i^\mathrm{shift}=\mathrm{Normalize}(\mathbf{x}_i - \lambda \vec{\Delta}_{\mathrm{gap}}) \\
\mathbf{y}_i^\mathrm{shift}=\mathrm{Normalize}(\mathbf{y}_i + \lambda \vec{\Delta}_{\mathrm{gap}})
\end{array}
$$

CLIP模型學習到的溫度$\tau$=0.01，在MSCOCO驗證集上計算得到的間隔$||\vec{\Delta}_{\mathrm{gap}}||$=0.82。

由下圖可知，$||\vec{\Delta}_{\mathrm{gap}}||$=0.82時在驗證集得到的損失最小；溫度爲1時，傾向於縮小間隔。

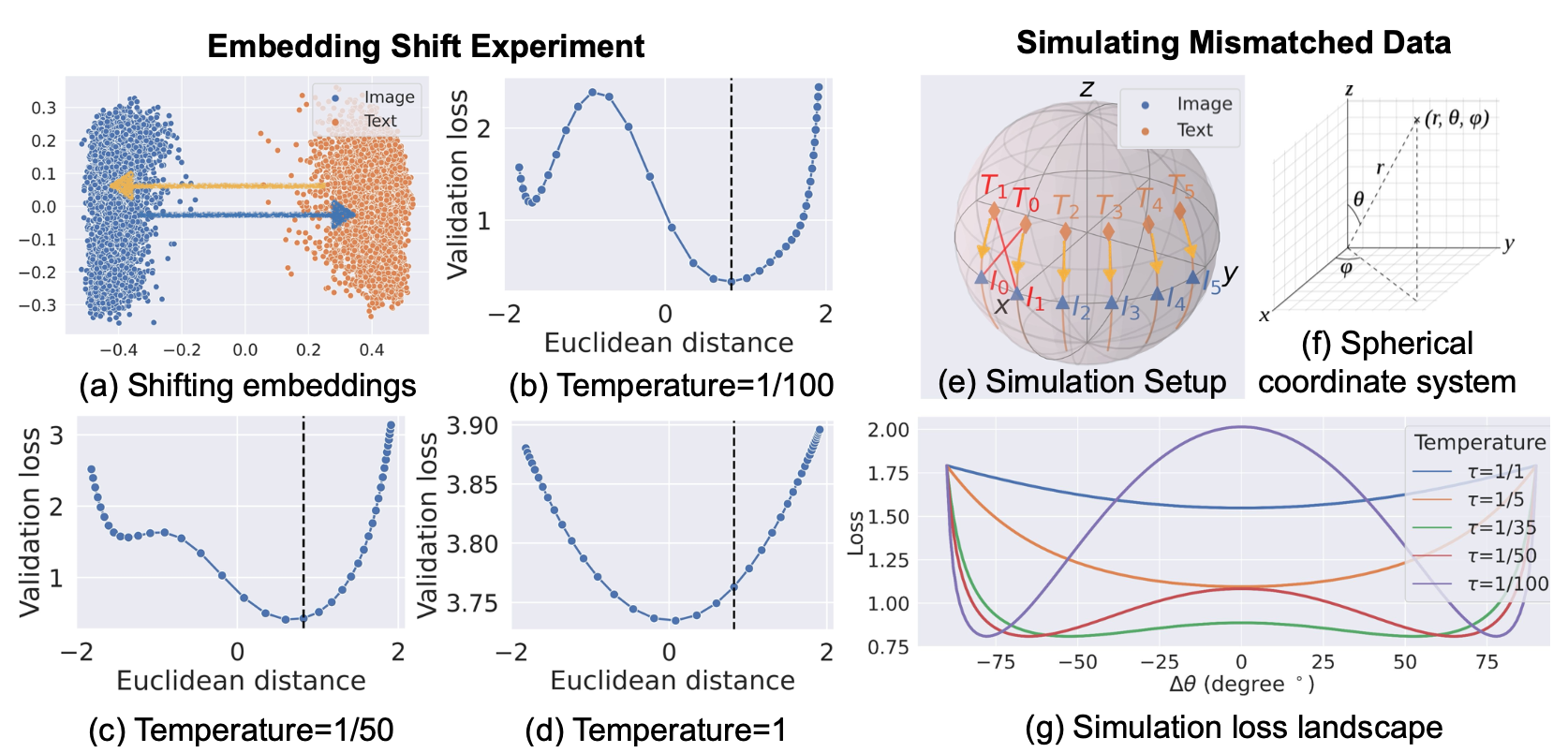
Contrastive learning preserves modality gap

進一步微調實驗證實，較大的溫度（$\tau\in \{ \frac{1}{10}, 1 \}$）縮小了間隔。

Reduce the gap by fine-tuning with high temperature

3維球坐標上存在部分不匹配圖文對（如圖中$T_1$和$I_0$更近）的模擬實驗也證明：設定較小溫度時，只有在球坐標上保持一定的角度差距，纔能使損失最低；設定較大的溫度則無此現象。額外的模擬實驗說明，如果圖文完全匹配則無此現象。

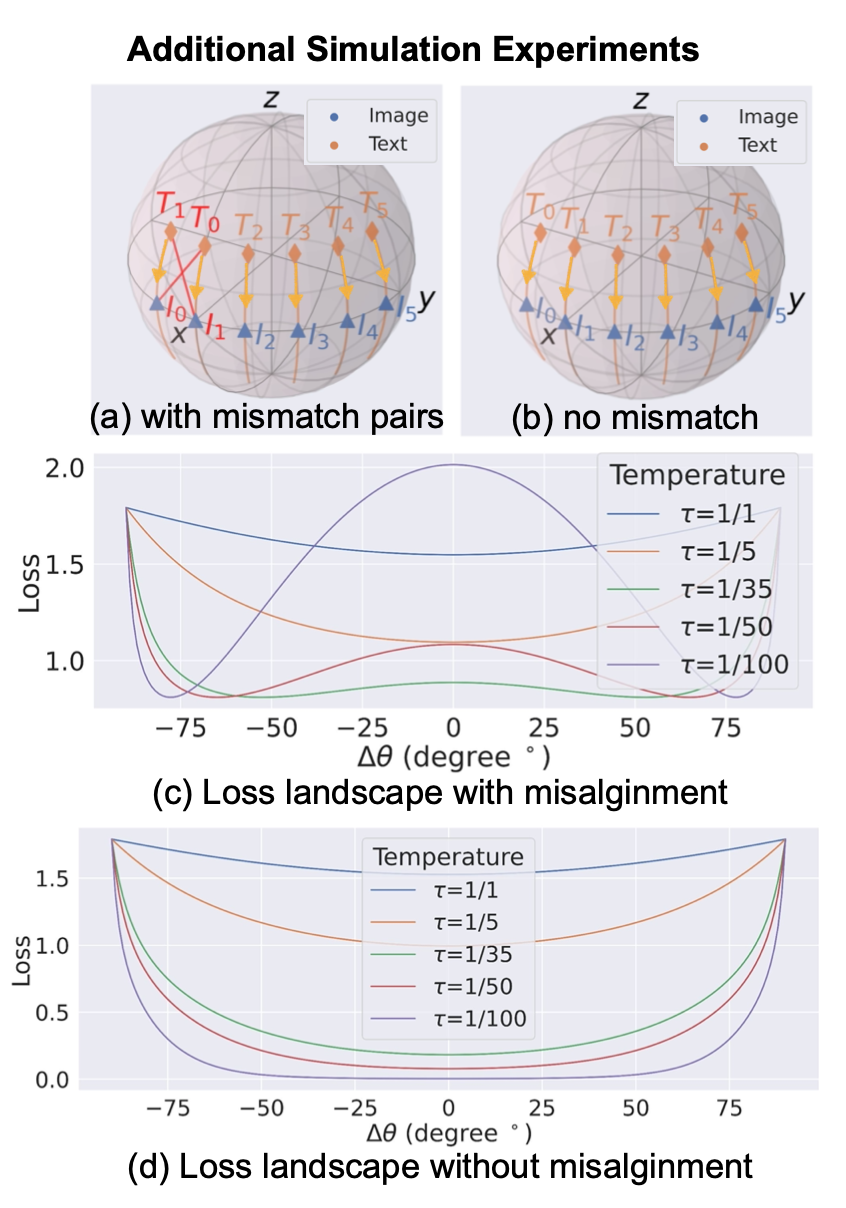
with and without mismatched data

初始化和優化的共同作用

另有CLIP訓練實驗，一採用隨機初始化，模態間隔 $||\vec{\Delta}_{\mathrm{gap}}|| = 1.1891 \pm 0.0017$；一將文本模態通過線性變換拉近至$||\vec{\Delta}_{\mathrm{gap}}|| = 0.0388 ± 0.0351$。訓練後：1.1891±0.0017變1.2991±0.0389，0.0388±0.0351變0.7457±0.0633。

結論：初始化和優化共同導致模態間隔。即使初始化幾乎無間隔，對比學習損失函數的優化仍然造成間隔，儘管間隔較小。

實驗

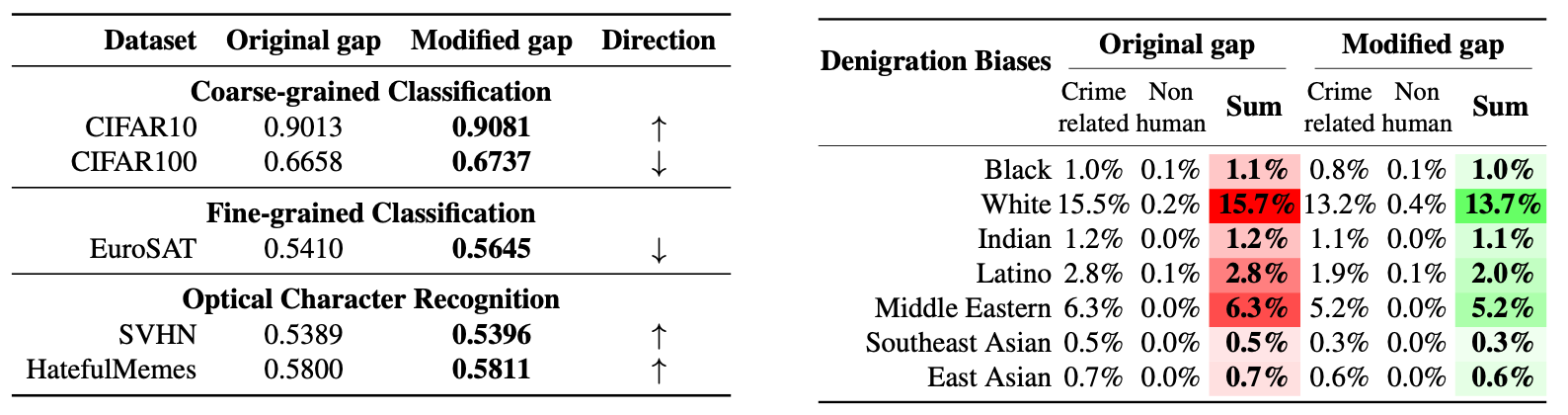
Experiments

適當調整模態間隔，有助於調整模型zero-shot性能，可減少模型在人臉識別任務上的種族偏見。間隔太小：犯罪相關偏見；間隔太大：非人類偏見。